Při přepočtu výstupních dat magnetografu na fyzikální jednotky vycházíme z kalibračních křivek, získaných na základě teoretických modelů sluneční atmosféry aplikací na konkrétní pozorovací podmínky a vlastnosti přístroje. Tyto tzv. kalibrační výpočty odlišujeme od korekčních výpočtů, sloužících k odstranění efektů (např. zklenutí jasového pole), komplikujících zobrazení zkoumaných fyzikálních parametrů. Metody kalibrace a korekce závisejí na zpracovávaném fyzikálním parametru.

JASOVÉ KANÁLY

Měřené intensity jsou lineární závislostí měřeného signálu na jasu, proto se zde kalibrační výpočty neprovádějí. Z korekčních důvodů pro jasové kanály používáme:

a)	Korekce změny průzračnosti atmosféry Intenzita měřeného místa I(i,j) aktivní oblasti je korigována na změny intenzity záření ve středu disku Is(t) vůči kalibrační hodnotě Is(0). Ik=I(i, j).Is(0)/Is(t), kde Ik(i,j) je korigovaná hodnota jasu j-tého řádku a i-tého sloupce mapy t je čas od počátku měření do okamžiku měření daného bodu (i,j) Is(0) hodnota jasu středu disku pro čas měření t=0 Tato korekce odstraňuje ve značné míře změny průzračnosti atmosféry.
b)	Korekce zklenutí jasového pole Korigovanými hodnotami jasového pole Ik(i,j) podle bodu a) je po řádcích proložena obalová křivka metodou odvalování přímky tak, aby se žádný měřený bod nenacházel nad obalovou křivkou. Obalové křivky tak vytváří referenční pole jasů klidné fotosféry Ir(i,j), vůči němuž je možno korigovat zklenutí pole.
c)	Přepočet jasu na kontrast Ve většině případů je vhodnější místo jasového pole Ik(i,j) pracovat s polem kontrastu C(i,j), které je definováno pro každý bod pole jako rozdíl mezi intenzitou referenčního pole a korigovanou měřenou intenzitou. C(i, j)=Ir(i, j)-Ik(i, j)
d)	Normování jasového pole Pro vzájemné porovnávání obrazů fotosféry je vhodné data, zpracovaná předcházejícími způsoby, normovat. Při normování pokládáme body normované referenční křivky IrN=10000 pro všechny body pole. Normovaná hodnota korigovaného jasu IkN(i,j) bude: IkN(i, j)=Ik(i, j).IrN/Ir(i, j)
e)	Normování kontrastu Analogicky bodu c) bude definováno normování kontrastu CN(i,j)=IrN-IkN(i,j) Tento parametr je vhodný pro další práci, zobrazování skvrn, výpočet rozptýleného světla, určování hranic skvrny a klidné fotosféry a pod.
f)	Korekce na rozptýlené světlo Jedná se o přibližnou korekci, vycházející z předpokladu, že jas v umbře velké skvrny by měl být menší než 10% jasu okolní fotosféry. Pokud minimální jas ve skvrně neodpovídá předpokládané hodnotě, je možno velmi jednoduše provést tuto korekci v poli kontrastu. Kontrast, korigovaný na rozptýlené světlo CNRS(i,j) bude: CNRS(i, j)=CN.CNmax/CN(i, j)max kde CNmax - maximální hodnota normovaného kontrastu, která by měla být ve skvrně pozorována CN(i,j)max - max. hodnota normovaného kontrastu naměřená ve skvrně
g)	Určení hranice mezi skvrnou a klidnou fotosférou Tato hranice je potřebná při kalibraci magnetického pole, protože se zde používají různé modely sluneční atmosféry. Hranice je definována podmínkami: CNRS(i, j)>1000 oblast skvrny CNRS(i, j) < 1000 oblast fotosféry

KANÁLY MAGNETICKÉHO POLE

Magnetograf je uspořádán tak, že 1. kanál měří Stokesův parametr V v jednom křídle čáry a 2. kanálu je parametr V druhého křídla čáry. Elektronická inverze druhého kanálu je provedena z důvodů dalšího zpracování. Kalibrace obou kanálů podélné složky mag. pole se provádí odděleně, na základě dat, získaných při kalibraci magnetografu měřením kruhově polarizovaného světla. Pro každý z obou kanálů spočítáme kalibrační koeficient

KOEFKAL=(I_kal-I_okal)/(H_kal-H_okal).Z_kal/Z_mer, kde

I_kal a H_kal jsou údaje kanálu I a kanálu V Stokesmetru při kalibraci přes kruhový polarizátor

I_okal a H_okal jsou tytéž údaje se zavřenou štěrbinou

Z_kal - zesílení při kalibraci

Z_mer - zesílení při měření

Pro každý bod měřené mapy spočítáme hodnotu
X(i)=KOEFKAL.(H_i-H_o)/(I_i-I_o)
kde

H_i, I_i jsou údaje kanálů V a I Stokesmetru při měření

H_o, I_o jsou tytéž údaje se zavřenou štěrbinou

Podle převodních křivek na obr. 1, odvozených Staudem (1975) vypočteme velikost podélné složky vektoru magnetické indukce.
Výběr jedné z obou křivek pro každý bod mapy se přitom provádí na základě testu, uvedeného v odstavci g) Kalibrace jasových kanálů
Porovnání výsledků z obou křídel spektrální čáry ukázala, že dochází ke vzdájemnému posuvu nuly, způsobenému zřejmě eliptickou polarizací světla na coelostatu. K odstranění tohoto posuvu jsou při zpracování kanálů mag. pole používány následující korekce:

a)	vzájemný posuv nuly obou datových souborů tak, aby počet bodů stejných polarit v obou mapách byl stejný (režim "P")
b)	pro každý bod výsledné mapy je spočítána hodnota magnetického pole z průměru magnetických polí obou kanálů (režim "M")
c)	pro každý bod výsledné mapy je spočítána hodnota magnetického pole z průměru změřených Stokesových parametrů obou kanálů (režim "S").

Praktické zkušenosti s těmito režimy ukázaly, že přes různé principy korekcí se výsledné datové soubory navzájem téměř neliší a proto se z hlediska rychlosti zpracování nejčastěji používá režim "S".
Protože tento princip i teoreticky odstraňuje uspokojivě parazitní eliptickou polarizaci, předpokládáme, že poloha nuly datového pole je reálná.

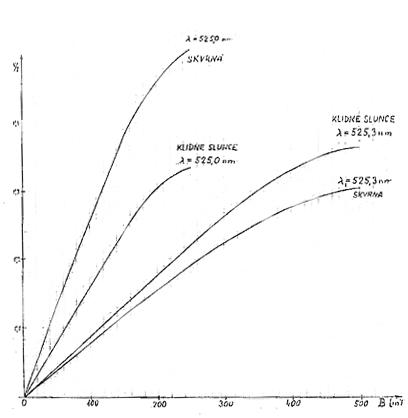
Závislost Stokesových parametrů V/I na longitudální složce magnetické indukce B_L pro dvě spektrální čáry. Pro skvrnu je použit model Stelbmacher-Wiehr a pro klidné Slunce model HSRA-Gingerich.

DOPPLEROVSKÉ RYCHLOSTI

Signály kanálu dopplerovských rychlostí jsou úměrné úhlu pootočení planparalelní destičky kompenzátoru, dostavujícího spektrální čáru symetricky na blok výstupních štěrbin s fotonásobiči. Vzhledem k malé odchylce od linearity překpokládáme, že měřená dopplerovská rychlost

v_D=(126D-v(i)).14/D [m/s]
kde

D je integrační koeficient měření

v(i) - údaj A/D převodníku v kanálu 8 pro konkrétní bod měřené oblasti

Vzhledem k vysoké rychlosti skanování při měření a určité setrvačnosti mechanického kompenzátoru jsme jeho funkci vylepšili matematickou korekcí, vycházející z nezkompenzovaného signálu jasu v obou křídlech spektrální čáry. Tato korekce je natolik dokonalá, že dokážeme rekonstruovat pole dopplerovských rychlostí v_kor(i) i v případě vypnutého kompenzátoru, kdy měření rychlostí neprobíhá.
v_kor(i)=v_D-DKOR(i),
kde korekční posuv
DKOR(i)=D_o(I₁(i)-I₂(i)K₂)/(I₁(i)6I₂(i)K₂) (*)
D_o = 20000 byl stanoven měřením a charakterizuje citlivost kompenzačního systému
K₂ = SI₁(i)/SI₂(i) odstraňuje datovou nesymetrii kompenzačních jasových kanálů I₁ a I₂.
Pokud zanedbáme změnu profilu spektrální čáry při přechodu z klidné fotosféry do umbry skvrny, můžeme říci, že tato matematická korekce nezávisí na jasu (viz výraz (*)), tzn. že na rozdíl od nedokonalého opticko-mechanického kompenzátoru funguje dokonale i ve skvrnách.
Lokální dopplerovské rychlosti jsou superponovány na rychlosti vzájemného pohybu pozorovacího stanoviště a pozorovaného místa. U malých aktivních oblastí vzhledem ke krátké době měření (5 min) je změna vzájemné rychlosti obou bodů s dostatečnou přesností reprezentována carringtonovskou rotací slunečního povrchu a proto na tuto rotaci provádíme matematickou korekci. Výsledná data ve většině případů reprezentují s dostatečnou přesností lokální dopplerovské rychlosti.
U velkých oblastí, zasahujících více než polovinu plochy Slunce se vzhledem k době trvání měření (40 min) již projevují i další vlivy, které bude nutno kompenzovat. Vzhledem k tomu, že uvedená dopplerovská měření nejsou absolutní, není zabezpečena přesná poloha nuly. Pro její určení proto používáme předpokladu, že integrální tok přes celou měřenou oblast by mohl být nulový, případně máme možnost celé datové pole potřebným směrem posunout. Není však vyloučeno, že v budoucnosti povede potřeba přesného stanovení nuly v kanálu rychlostí k absolutním měřením.

LITERATURA

Klvaňa, M.; Bumba, V.: 1993, Kalibrace magnetografických měření, Zborník referátov z 11. celoštátného slnečného seminára, B. Lukáč (ed), SÜH Hurbanovo, 12-14
Staude, J.; Bachmann G.; Jäger F. W.; Künzel H.; Pflug K.: 1975, HHI-STP-Report No 4, Berlin